更多+ 新闻
更多+ 通知公告
- 04.08西安交通大学电信学部电子学院202...
- 04.07电子与信息学部2023-2024学年第二...
- 04.03电子与信息学部电子科学与工程学...
- 04.02电子学院2024年硕士研究生招生考...
- 03.20电信学部-陈妮妮UNl微密weme圈2024...
- 12.14电子与信息学部电子科学与工程学...
- 10.18西安交通大学电信学部电子学院202...
- 10.132024年电信学部电子科学与工程学...
- 10.132023年陈妮妮UNl微密weme圈 “研究...
更多+ 本科生教育
- 07-09电子科学与技术专业培养方案
- 07-09西安交通大学鼓励学生参加学科/...
- 07-09西安交通大学鼓励学生参加学科/...
- 01-03西安交通大学优秀本科生提前进...
- 01-03等待更新
- 01-03等待更新
- 01-03等待更新
更多+ 研究生教育
- 06-10电子与信息学部硕士学位申请实...
- 06-19关于陈妮妮UNl微密weme圈2022年...
- 06-02电信学部-陈妮妮UNl微密weme圈20...
- 10-29西安交通大学2022年硕士研究生...
- 10-29西安交通大学2022年硕士研究生...
- 10-29西安交通大学2022年电子学院硕...
- 06-10电子与信息学部硕士学位申请实...
- 05-21电信学部陈妮妮UNl微密weme圈202...
更多+ 研究动态
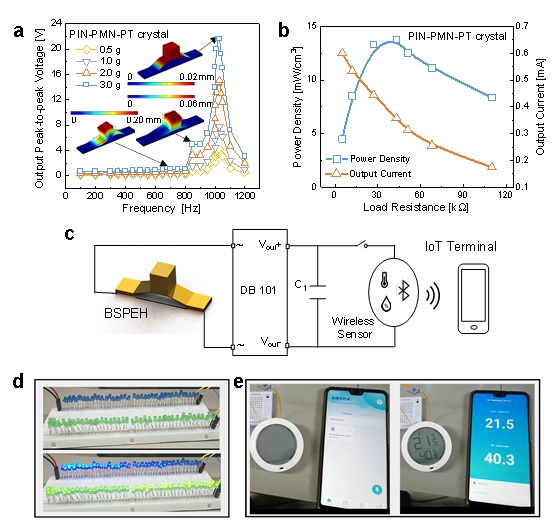
- 11-29交大科研人员最新科研成果在Remot...
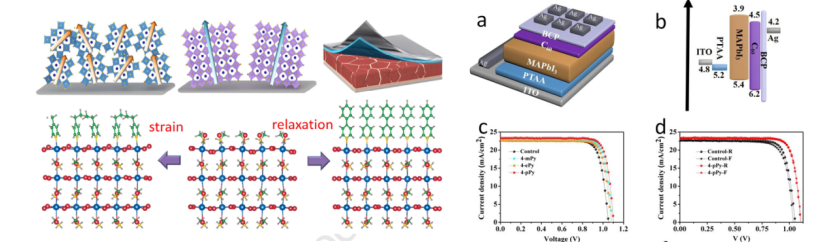
- 06-02交大科研人员实现基于表面晶格应...
- 05-29西安交通大学研究人员开发出新型...
- 10-13任巍教授团队论文获得美国陶瓷学...
- 07-10西安交大科研人员设计共轭配体分...